El análisis experimental de algoritmos de ordenamiento es fundamental en la computación y la ciencia de datos. Estos algoritmos son utilizados en diversas aplicaciones, como bases de datos, análisis de grandes volúmenes de datos y sistemas operativos. En este trabajo, se analizan cinco algoritmos de ordenamiento basados en comparación: Heapsort, Mergesort, Quicksort, Bubblesort y Skiplist. Estos algoritmos presentan diferentes complejidades computacionales y eficiencia en distintos escenarios (Cormen et al. 2009).
El ordenamiento es una operación esencial en la manipulación de datos, ya que permite la búsqueda eficiente, la optimización de estructuras de datos y la mejora en el rendimiento de consultas en bases de datos. La eficiencia de estos algoritmos varía dependiendo de factores como la distribución inicial de los datos y el acceso a memoria. Mientras que algoritmos como Mergesort son eficientes y estables, requieren memoria adicional, lo que los hace menos adecuados para sistemas con restricciones de memoria. Por otro lado, Quicksort es rápido en la práctica, pero su rendimiento puede degradarse en ciertos casos (Knuth 1998).
Uno de los principales desafíos en el uso de estos algoritmos es su complejidad computacional, ya que el número de comparaciones y movimientos de elementos varía considerablemente entre ellos. Evaluar su rendimiento implica medir tanto el tiempo de ejecución como la cantidad de comparaciones realizadas. Además, el uso de estructuras de datos como Skiplist introduce una perspectiva diferente sobre la eficiencia en el ordenamiento, ya que utiliza niveles de listas enlazadas para mejorar la velocidad de búsqueda y manipulación de datos (Pugh 1990).
El objetivo principal de este estudio es evaluar el rendimiento de estos algoritmos de ordenamiento en términos de tiempo de ejecución y número de comparaciones, utilizando conjuntos de datos con diferentes niveles de desorden. Se analizarán las ventajas y desventajas de cada algoritmo en función de su eficiencia en distintos escenarios computacionales (Sedgewick y Wayne 2011).
6 Metodología
Los algoritmos analizados en este reporte son:
Heapsort: Algoritmo basado en estructuras de montículos (heaps) que ordena extrayendo elementos del heap máximo, el orden de crecimiento de Heapsort es de O(n log n)
Mergesort: Algoritmo de ordenamiento basado en dividir y conquistar, que divide el conjunto en mitades y luego las combina ordenadamente. Igual que Heapsort tiene un nivel de complejidad de O (n log n).
Quicksort: Algoritmo recursivo que selecciona un pivote y divide el conjunto en dos partes, ordenándolas de manera independiente. Es uno de los agloritmos más rapidos en la práctica y su orden de crecimiento en promedio tambien es de O(n log n)
Bubblesort: Algoritmo simple pero ineficiente que intercambia elementos adyacentes repetidamente hasta que la lista está ordenada. Su orden de crecimiento es de O(n^2)
Skiplist Sort: Algoritmo basado en la estructura de Skiplist, que permite ordenamiento eficiente aprovechando múltiples niveles de listas enlazadas.
Los algoritmos se evaluarán utilizando diferentes conjuntos de datos provenientes de archivos JSON, los cuales contienen listas con distintos niveles de desorden. Para la evaluación de los algoritmos se medirán separadamente el tiempo de ejecución y el número de comparaciones realizadas para cada lista con su distinto nivel de desorden.
7 Código utilizado
Código
import timeimport jsonimport matplotlib.pyplot as pltimport numpy as npimport pandas as pdimport randomdef heapsort(arr): comparisons = [0]def heapify(arr, n, i): largest = i l =2* i +1 r =2* i +2if l < n and arr[l] > arr[largest]: largest = l comparisons[0]+=1if r < n and arr[r] > arr[largest]: largest = r comparisons[0]+=1if largest != i: arr[i], arr[largest] = arr[largest], arr[i] heapify(arr, n, largest) n =len(arr)for i inrange(n //2-1, -1, -1): heapify(arr, n, i)for i inrange(n -1, 0, -1): arr[i], arr[0] = arr[0], arr[i] heapify(arr, i, 0)return comparisons[0]def mergesort(arr): comparisons = [0]def merge(l, m, r): L = arr[l:m+1] R = arr[m+1:r+1] i = j =0 k = lwhile i <len(L) and j <len(R): comparisons[0] +=1if L[i] <= R[j]: arr[k] = L[i] i +=1else: arr[k] = R[j] j +=1 k +=1while i <len(L): arr[k] = L[i] i +=1 k +=1while j <len(R): arr[k] = R[j] j +=1 k +=1def mergesort_rec(l, r):if l < r: m = (l + r) //2 mergesort_rec(l, m) mergesort_rec(m +1, r) merge(l, m, r) mergesort_rec(0, len(arr) -1)return comparisons[0]def quicksort(arr): comparisons = [0]def partition(low, high): pivot = arr[high] # último elemento como pivote i = lowfor j inrange(low, high): comparisons[0] +=1if arr[j] <= pivot: arr[i], arr[j] = arr[j], arr[i] i +=1 arr[i], arr[high] = arr[high], arr[i]return idef quicksort_rec(low, high):if low < high: pi = partition(low, high) quicksort_rec(low, pi -1) quicksort_rec(pi +1, high) quicksort_rec(0, len(arr) -1)return comparisons[0]def bubblesort(arr): comparisons =0 n =len(arr)for i inrange(n): swapped=Falsefor j inrange(0, n - i -1): comparisons +=1if arr[j] > arr[j +1]: arr[j], arr[j +1] = arr[j +1], arr[j] swapped =Trueifnot swapped: breakreturn comparisonsclass Node:def__init__(self, key, level):self.key = keyself.forward = [None] * (level +1)class SkipList:def__init__(self, max_level=16, p=0.5):self.max_level = max_levelself.p = pself.header = Node(-1, max_level)self.level =0self.comparisons =0def random_level(self): lvl =0while random.random() <self.p and lvl <self.max_level: lvl +=1return lvldef insert(self, key): update = [None] * (self.max_level +1) current =self.headerfor i inrange(self.level, -1, -1):while current.forward[i] and current.forward[i].key < key:self.comparisons +=1 current = current.forward[i] update[i] = current lvl =self.random_level()if lvl >self.level:for i inrange(self.level +1, lvl +1): update[i] =self.headerself.level = lvl node = Node(key, lvl)for i inrange(lvl +1): node.forward[i] = update[i].forward[i] update[i].forward[i] = nodedef to_list(self): arr = [] current =self.header.forward[0]while current: arr.append(current.key) current = current.forward[0]return arrdef skiplistsort(arr): skiplist = SkipList()for num in arr: skiplist.insert(num)return skiplist.comparisons def load_data(file_path):withopen(file_path, 'r') as f: data = json.load(f)return data['reunion']def evaluate_algorithms(files): results = []forfilein files: arr = load_data(file)for alg in [heapsort, mergesort, quicksort,skiplistsort,bubblesort]: arr_copy = arr.copy() start_time = time.time() comparisons = alg(arr_copy) elapsed_time = time.time() - start_time results.append((file, alg.__name__, elapsed_time, comparisons))return pd.DataFrame(results, columns=['Archivo', 'Algoritmo','Tiempo', 'Comparaciones'])def generate_latex_table(df, filename): latex_table = df.to_latex(index=False) latex_table ="""\\begin{table}[ht]\\caption{Resultados de tiempos de ejecucion y operaciones}\\label{tab:results}\\centering"""+ latex_table +"""\\end{table}"""withopen(filename, 'w') as f: f.write(latex_table)def plot_results(df): plt.figure(figsize=(10, 5))for alg in df['Algoritmo'].unique(): subset = df[df['Algoritmo'] == alg] plt.plot(subset['Archivo'], subset['Tiempo'], label=alg) plt.xlabel("Archivo") plt.ylabel("Tiempo (s)") plt.legend() plt.grid() plt.savefig("tiempos_algoritmos.png")def plot_operaciones(df): plt.figure(figsize=(10, 5))for alg in df['Algoritmo'].unique(): subset = df[df['Algoritmo'] == alg] plt.plot(subset['Archivo'], subset['Comparaciones'], label=alg) plt.xlabel("Archivo") plt.ylabel("Operaciones") plt.legend() plt.grid() plt.savefig("ops_algoritmos.png")def plot_results_without_bubblesort(df): plt.figure(figsize=(10, 5))for alg in df['Algoritmo'].unique():if alg !="bubblesort": subset = df[df['Algoritmo'] == alg] plt.plot(subset['Archivo'], subset['Tiempo'], marker='o', label=alg) plt.xlabel("Archivo") plt.ylabel("Tiempo (s)") plt.legend() plt.grid() plt.xticks(rotation=45) plt.savefig("tiempos_algoritmos_sin_bubblesort.png")def plot_operaciones_without_bubblesort(df): plt.figure(figsize=(10, 5))for alg in df['Algoritmo'].unique():if alg !="bubblesort": subset = df[df['Algoritmo'] == alg] plt.plot(subset['Archivo'], subset['Comparaciones'], marker='o', label=alg) plt.xlabel("Archivo") plt.ylabel("Número de Comparaciones") plt.legend() plt.grid() plt.xticks(rotation=45) plt.savefig("ops_algoritmos_sin_bubblesort.png")files = ["P=016.json", "P=032.json", "P=064.json", "P=128.json", "P=256.json", "P=512.json"]df_results = evaluate_algorithms(files)df_time=df_results.pivot(index="Archivo", columns="Algoritmo", values="Tiempo")df_time.reset_index(inplace=True)generate_latex_table(df_time, 'resultados_tiempos.tex')df_comp=df_results.pivot(index="Archivo", columns="Algoritmo", values="Comparaciones")df_comp.reset_index(inplace=True)generate_latex_table(df_comp, 'resultados_comp.tex')plot_results(df_results)plot_operaciones(df_results)plot_results_without_bubblesort(df_results)plot_operaciones_without_bubblesort(df_results)
8 Analisis de Resultados
8.1 Tiempo de operación.
El análisis de los tiempos de operación de los algoritmos de ordenamiento revela diferencias significativas en su eficiencia. La Tabla\(\ref{tab:results}\) muestra los tiempos promedio de ejecución para cada algoritmo y cada conjunto de datos, mientras que las Figuras 1 y 2 presentan la comparación gráfica, destacando el impacto del tamaño del conjunto de datos en el rendimiento de cada algoritmo.
Como se observa en la Figura 1, el algoritmo Bubblesort exhibe un tiempo de ejecución significativamente mayor en comparación con los otros métodos, aumentando exponencialmente conforme crece el tamaño del archivo de entrada. Asi mismo, se observa una tendencia hacia arriba entre más desordenada este la lista. Este comportamiento se debe a su complejidad de \(O(n^2)\) en el peor caso, lo que lo hace poco eficiente para conjuntos de datos grandes y alto nivel de desorden (Cormen et al. 2009). Debido a esto, la Figura 2 excluye Bubblesort para mejorar la visualización de los otros algoritmos.
Comparación de Tiempo de ejecución entre algoritmos de ordenamiento
Entre los algoritmos restantes, Quicksort es el más rápido cuando P=512 ejecutandose en 0.013 segundos. Este resultado se debe a su eficiencia promedio de \(O(n \log n)\) y al hecho de que en la mayoría de los casos selecciona pivotes efectivos para dividir los datos Loeser (1974); Hoare (1962). Sin embargo, en el peor caso, cuando los datos están desbalanceados, su complejidad puede degradarse a \(O(n^2)\) [Sedgewick y Wayne (2011)]. En las listas evaluadas cuando P=016 y P=032 su complejidad se lego a degradar llegando hasta un tiempo de ejecución de 0.21 segundos
Comparación de Tiempo de ejecución entre algoritmos de ordenamiento (Sin Bubble Sort)
Mergesort presenta tiempos de ejecución ligeramente superiores a los de Quicksort, pero se mantiene en el mismo orden de magnitud. Su ventaja principal radica en su estabilidad y en su rendimiento predecible de \(O(n \log n)\) en todos los casos, lo que lo hace ideal para aplicaciones donde la estabilidad es crítica, como la ordenación de registros de bases de datos (Knuth 1998). Se nota una tendencia a incrementar el tiempo de ejecución conforme va aumentando el nivel de desorden de los datos.
Heapsort muestra tiempos de ejecución consistentes, pero es ligeramente más lento que Quicksort y Mergesort. Esto se debe a las operaciones de heapify, que introducen una mayor cantidad de operaciones en la manipulación de los datos, y tambien se nota un poco de mayor de tiempo en niveles de desorden bajos. Aunque su peor caso sigue siendo \(O(n \log n)\), su overhead adicional lo hace menos competitivo en comparación con los otros métodos (Cormen et al. 2009).
Finalmente, el algoritmo basado en SkipList tiene tiempos de ejecución intermedios, siendo más lento que Quicksort y Mergesort, pero similar a Heapsort, y se nota una tendencia estable en el tiempo de ejecución conforme va a aumentando el nivel de desorden de las listas. Esto se debe a la naturaleza probabilística de las listas enlazadas con múltiples niveles, las cuales requieren más operaciones para ordenar los datos (Pugh 1990). A pesar de ello, su rendimiento sigue siendo eficiente para estructuras dinámicas donde la inserción y búsqueda rápida son cruciales.
8.2 Número de Comparaciones
El número de comparaciones es una métrica crucial para evaluar la eficiencia de los algoritmos de ordenamiento, ya que está directamente relacionado con la complejidad computacional de cada método. En la Tabla\(\ref{tab:results1}\) se presentan los valores obtenidos para cada algoritmo en distintos tamaños de archivos, mientras que las Figuras 3 y 4 muestran la comparación gráfica de estas operaciones.
Como se observa en la Figura 3, el algoritmo Bubblesort realiza un número extremadamente alto de comparaciones en comparación con los otros métodos. Su crecimiento cuadrático, con una complejidad de \(O(n^2)\), provoca que el número de comparaciones aumente exponencialmente a medida que el tamaño del conjunto de datos se incrementa (Cormen et al. 2009), pero en este caso se llega a estabilizar en alrededor de 470000 sin importar el nivel de desorden de los datos. Debido a esta magnitud del Número de comparaciones, la Figura 4 excluye Bubblesort para resaltar mejor el comportamiento de los otros algoritmos.
Comparación de Número de Comparaciones entre algoritmos de ordenamiento
Entre los algoritmos restantes, Mergesort es el que realiza el menor número de comparaciones en todos los casos, lo que se debe a su estrategia de dividir y conquistar, logrando un rendimiento estable de \(O(n \log n)\) en todos los escenarios (Knuth 1998). Esto confirma su idoneidad para situaciones donde el número de comparaciones es un factor limitante, como en el procesamiento de grandes volúmenes de datos en bases de datos y sistemas de archivos (Sedgewick y Wayne 2011). De igual manera que con el tiempo de ejecución se observa un número de operaciones con tendencia a la alza conforme el nivel de desorden de los datos va aumentando.
Comparación de Número de Comparaciones entre algoritmos de ordenamiento (Sin Bubble Sort)
Por otro lado, Quicksort presenta un número de comparaciones en comparación con los demás algoritmos (excluyendo a Bubble Sort), pero sigue siendo bastante eficiente cuando las listas se van aumentando su nivel de desorden. Su complejidad promedio de \(O(n \log n)\) lo hace competitivo, aunque en su peor caso puede alcanzar \(O(n^2)\) si los pivotes seleccionados no dividen bien los datos (Hoare 1962), este caso se presenta niveles bajos de desorden de las listas. En este caso el número de comparaciones va disminuyendo conforme P va aumentando en las listas.
Heapsort realiza un número de comparaciones mayor que Quicksort y Mergesort, lo que se debe a la naturaleza de la estructura de montículo utilizada para mantener el orden de los elementos. Su comportamiento es consistente y su peor caso sigue siendo \(O(n \log n)\), pero su mayor número de comparaciones lo hace menos competitivo en comparación con los otros métodos (Cormen et al. 2009). Se nota una tendencia estable conforme va aumentando el nivel de desorden de las listas.
El algoritmo SkipListSort muestra un comportamiento más variable en términos de comparaciones, con fluctuaciones en distintos tamaños de datos y niveles de desorden. Esto se debe a la naturaleza probabilística de las listas enlazadas en múltiples niveles, que introducen cierta incertidumbre en el número de operaciones requeridas para ordenar los elementos (Pugh 1990). A pesar de estas variaciones, su número de comparaciones sigue siendo relativamente cercano a los otros algoritmos eficientes y es significativamente menor que el de Bubblesort.
9 Conclusión
En conclusión, Quicksort es el algoritmo más eficiente en términos de tiempo de ejecución cuando las listas presentan alto nivel de desorden. Para el caso de Mergesort y Heapsort son medianamente eficientes y el nivel de desorden no afecta degrada su complejidad. SkipListSort se comporta de manera aceptable, pero no es tan eficiente como los métodos clásicos de comparación. Bubblesort, en contraste, es altamente ineficiente y se vuelve impráctico para grandes volúmenes de datos. Estos resultados coinciden con estudios previos sobre la eficiencia de los algoritmos de ordenamiento y confirman la superioridad de los métodos basados en división y conquista para el procesamiento eficiente de datos (Sedgewick y Wayne 2011).
El análisis de comparaciones confirma que Bubblesort es altamente ineficiente, mientras que Mergesort y Quicksort son los métodos más efectivos en términos de reducir el número de operaciones. Heapsort tiene un desempeño estable pero menos competitivo, y SkipListSort muestra variabilidad en su número de comparaciones debido a su estructura de datos probabilística. Estos resultados refuerzan los estudios previos sobre la eficiencia de los algoritmos de ordenamiento y su aplicabilidad en distintos escenarios computacionales (Sedgewick y Wayne 2011).
##Lista de Cambios
Se implementó quicksort in-place usando el esquema de partición de Lomuto, con el último elemento como pivote.
Se implementó mergesort in-place usando índices, evitando la creación de nuevas listas en cada llamada recursiva.
Cambios en Analisis de Resultados asi como conclusiones con nuevos resultados de Quicksort y Merge Sort
10 Bibliografía
Cormen, Thomas H., Charles E. Leiserson, Ronald L. Rivest, y Clifford Stein. 2009. Introduction to Algorithms, Third Edition. MIT Press.
---title: "3A. Reporte escrito. Experimentos y análisis de algoritmos de ordenamiento."author: "José Francisco Cázares Marroquín"date: "03/01/2025"format: html: toc: true lang: es-MX number-sections: true code-fold: true theme: cosmo css: styles.cssexecute: echo: true eval: false warning: falsebibliography: references.bib---# IntroducciónEl análisis experimental de algoritmos de ordenamiento es fundamental en la computación y la ciencia de datos. Estos algoritmos son utilizados en diversas aplicaciones, como bases de datos, análisis de grandes volúmenes de datos y sistemas operativos. En este trabajo, se analizan cinco algoritmos de ordenamiento basados en comparación: Heapsort, Mergesort, Quicksort, Bubblesort y Skiplist. Estos algoritmos presentan diferentes complejidades computacionales y eficiencia en distintos escenarios [@cormen2009].El ordenamiento es una operación esencial en la manipulación de datos, ya que permite la búsqueda eficiente, la optimización de estructuras de datos y la mejora en el rendimiento de consultas en bases de datos. La eficiencia de estos algoritmos varía dependiendo de factores como la distribución inicial de los datos y el acceso a memoria. Mientras que algoritmos como Mergesort son eficientes y estables, requieren memoria adicional, lo que los hace menos adecuados para sistemas con restricciones de memoria. Por otro lado, Quicksort es rápido en la práctica, pero su rendimiento puede degradarse en ciertos casos [@knuth1998].Uno de los principales desafíos en el uso de estos algoritmos es su complejidad computacional, ya que el número de comparaciones y movimientos de elementos varía considerablemente entre ellos. Evaluar su rendimiento implica medir tanto el tiempo de ejecución como la cantidad de comparaciones realizadas. Además, el uso de estructuras de datos como Skiplist introduce una perspectiva diferente sobre la eficiencia en el ordenamiento, ya que utiliza niveles de listas enlazadas para mejorar la velocidad de búsqueda y manipulación de datos [@pugh1990].El objetivo principal de este estudio es evaluar el rendimiento de estos algoritmos de ordenamiento en términos de tiempo de ejecución y número de comparaciones, utilizando conjuntos de datos con diferentes niveles de desorden. Se analizarán las ventajas y desventajas de cada algoritmo en función de su eficiencia en distintos escenarios computacionales [@sedgewick2011].# MetodologíaLos algoritmos analizados en este reporte son:1. **Heapsort**: Algoritmo basado en estructuras de montículos (heaps) que ordena extrayendo elementos del heap máximo, el orden de crecimiento de Heapsort es de O(n log n)2. **Mergesort**: Algoritmo de ordenamiento basado en dividir y conquistar, que divide el conjunto en mitades y luego las combina ordenadamente. Igual que Heapsort tiene un nivel de complejidad de O (n log n).3. **Quicksort**: Algoritmo recursivo que selecciona un pivote y divide el conjunto en dos partes, ordenándolas de manera independiente. Es uno de los agloritmos más rapidos en la práctica y su orden de crecimiento en promedio tambien es de O(n log n)4. **Bubblesort**: Algoritmo simple pero ineficiente que intercambia elementos adyacentes repetidamente hasta que la lista está ordenada. Su orden de crecimiento es de O(n\^2)5. **Skiplist Sort**: Algoritmo basado en la estructura de Skiplist, que permite ordenamiento eficiente aprovechando múltiples niveles de listas enlazadas.Los algoritmos se evaluarán utilizando diferentes conjuntos de datos provenientes de archivos JSON, los cuales contienen listas con distintos niveles de desorden. Para la evaluación de los algoritmos se medirán separadamente el tiempo de ejecución y el número de comparaciones realizadas para cada lista con su distinto nivel de desorden.# Código utilizado```{python}import timeimport jsonimport matplotlib.pyplot as pltimport numpy as npimport pandas as pdimport randomdef heapsort(arr): comparisons = [0]def heapify(arr, n, i): largest = i l =2* i +1 r =2* i +2if l < n and arr[l] > arr[largest]: largest = l comparisons[0]+=1if r < n and arr[r] > arr[largest]: largest = r comparisons[0]+=1if largest != i: arr[i], arr[largest] = arr[largest], arr[i] heapify(arr, n, largest) n =len(arr)for i inrange(n //2-1, -1, -1): heapify(arr, n, i)for i inrange(n -1, 0, -1): arr[i], arr[0] = arr[0], arr[i] heapify(arr, i, 0)return comparisons[0]def mergesort(arr): comparisons = [0]def merge(l, m, r): L = arr[l:m+1] R = arr[m+1:r+1] i = j =0 k = lwhile i <len(L) and j <len(R): comparisons[0] +=1if L[i] <= R[j]: arr[k] = L[i] i +=1else: arr[k] = R[j] j +=1 k +=1while i <len(L): arr[k] = L[i] i +=1 k +=1while j <len(R): arr[k] = R[j] j +=1 k +=1def mergesort_rec(l, r):if l < r: m = (l + r) //2 mergesort_rec(l, m) mergesort_rec(m +1, r) merge(l, m, r) mergesort_rec(0, len(arr) -1)return comparisons[0]def quicksort(arr): comparisons = [0]def partition(low, high): pivot = arr[high] # último elemento como pivote i = lowfor j inrange(low, high): comparisons[0] +=1if arr[j] <= pivot: arr[i], arr[j] = arr[j], arr[i] i +=1 arr[i], arr[high] = arr[high], arr[i]return idef quicksort_rec(low, high):if low < high: pi = partition(low, high) quicksort_rec(low, pi -1) quicksort_rec(pi +1, high) quicksort_rec(0, len(arr) -1)return comparisons[0]def bubblesort(arr): comparisons =0 n =len(arr)for i inrange(n): swapped=Falsefor j inrange(0, n - i -1): comparisons +=1if arr[j] > arr[j +1]: arr[j], arr[j +1] = arr[j +1], arr[j] swapped =Trueifnot swapped: breakreturn comparisonsclass Node:def__init__(self, key, level):self.key = keyself.forward = [None] * (level +1)class SkipList:def__init__(self, max_level=16, p=0.5):self.max_level = max_levelself.p = pself.header = Node(-1, max_level)self.level =0self.comparisons =0def random_level(self): lvl =0while random.random() <self.p and lvl <self.max_level: lvl +=1return lvldef insert(self, key): update = [None] * (self.max_level +1) current =self.headerfor i inrange(self.level, -1, -1):while current.forward[i] and current.forward[i].key < key:self.comparisons +=1 current = current.forward[i] update[i] = current lvl =self.random_level()if lvl >self.level:for i inrange(self.level +1, lvl +1): update[i] =self.headerself.level = lvl node = Node(key, lvl)for i inrange(lvl +1): node.forward[i] = update[i].forward[i] update[i].forward[i] = nodedef to_list(self): arr = [] current =self.header.forward[0]while current: arr.append(current.key) current = current.forward[0]return arrdef skiplistsort(arr): skiplist = SkipList()for num in arr: skiplist.insert(num)return skiplist.comparisons def load_data(file_path):withopen(file_path, 'r') as f: data = json.load(f)return data['reunion']def evaluate_algorithms(files): results = []forfilein files: arr = load_data(file)for alg in [heapsort, mergesort, quicksort,skiplistsort,bubblesort]: arr_copy = arr.copy() start_time = time.time() comparisons = alg(arr_copy) elapsed_time = time.time() - start_time results.append((file, alg.__name__, elapsed_time, comparisons))return pd.DataFrame(results, columns=['Archivo', 'Algoritmo','Tiempo', 'Comparaciones'])def generate_latex_table(df, filename): latex_table = df.to_latex(index=False) latex_table ="""\\begin{table}[ht]\\caption{Resultados de tiempos de ejecucion y operaciones}\\label{tab:results}\\centering"""+ latex_table +"""\\end{table}"""withopen(filename, 'w') as f: f.write(latex_table)def plot_results(df): plt.figure(figsize=(10, 5))for alg in df['Algoritmo'].unique(): subset = df[df['Algoritmo'] == alg] plt.plot(subset['Archivo'], subset['Tiempo'], label=alg) plt.xlabel("Archivo") plt.ylabel("Tiempo (s)") plt.legend() plt.grid() plt.savefig("tiempos_algoritmos.png")def plot_operaciones(df): plt.figure(figsize=(10, 5))for alg in df['Algoritmo'].unique(): subset = df[df['Algoritmo'] == alg] plt.plot(subset['Archivo'], subset['Comparaciones'], label=alg) plt.xlabel("Archivo") plt.ylabel("Operaciones") plt.legend() plt.grid() plt.savefig("ops_algoritmos.png")def plot_results_without_bubblesort(df): plt.figure(figsize=(10, 5))for alg in df['Algoritmo'].unique():if alg !="bubblesort": subset = df[df['Algoritmo'] == alg] plt.plot(subset['Archivo'], subset['Tiempo'], marker='o', label=alg) plt.xlabel("Archivo") plt.ylabel("Tiempo (s)") plt.legend() plt.grid() plt.xticks(rotation=45) plt.savefig("tiempos_algoritmos_sin_bubblesort.png")def plot_operaciones_without_bubblesort(df): plt.figure(figsize=(10, 5))for alg in df['Algoritmo'].unique():if alg !="bubblesort": subset = df[df['Algoritmo'] == alg] plt.plot(subset['Archivo'], subset['Comparaciones'], marker='o', label=alg) plt.xlabel("Archivo") plt.ylabel("Número de Comparaciones") plt.legend() plt.grid() plt.xticks(rotation=45) plt.savefig("ops_algoritmos_sin_bubblesort.png")files = ["P=016.json", "P=032.json", "P=064.json", "P=128.json", "P=256.json", "P=512.json"]df_results = evaluate_algorithms(files)df_time=df_results.pivot(index="Archivo", columns="Algoritmo", values="Tiempo")df_time.reset_index(inplace=True)generate_latex_table(df_time, 'resultados_tiempos.tex')df_comp=df_results.pivot(index="Archivo", columns="Algoritmo", values="Comparaciones")df_comp.reset_index(inplace=True)generate_latex_table(df_comp, 'resultados_comp.tex')plot_results(df_results)plot_operaciones(df_results)plot_results_without_bubblesort(df_results)plot_operaciones_without_bubblesort(df_results)```# Analisis de Resultados## Tiempo de operación.El análisis de los tiempos de operación de los algoritmos de ordenamiento revela diferencias significativas en su eficiencia. La **Tabla** \ref{tab:results} muestra los tiempos promedio de ejecución para cada algoritmo y cada conjunto de datos, mientras que las **Figuras 1 y 2** presentan la comparación gráfica, destacando el impacto del tamaño del conjunto de datos en el rendimiento de cada algoritmo.\input{resultados_tiempos.tex}Como se observa en la **Figura 1**, el algoritmo **Bubblesort** exhibe un tiempo de ejecución significativamente mayor en comparación con los otros métodos, aumentando exponencialmente conforme crece el tamaño del archivo de entrada. Asi mismo, se observa una tendencia hacia arriba entre más desordenada este la lista. Este comportamiento se debe a su complejidad de $O(n^2)$ en el peor caso, lo que lo hace poco eficiente para conjuntos de datos grandes y alto nivel de desorden [@cormen2009]. Debido a esto, la **Figura 2** excluye Bubblesort para mejorar la visualización de los otros algoritmos.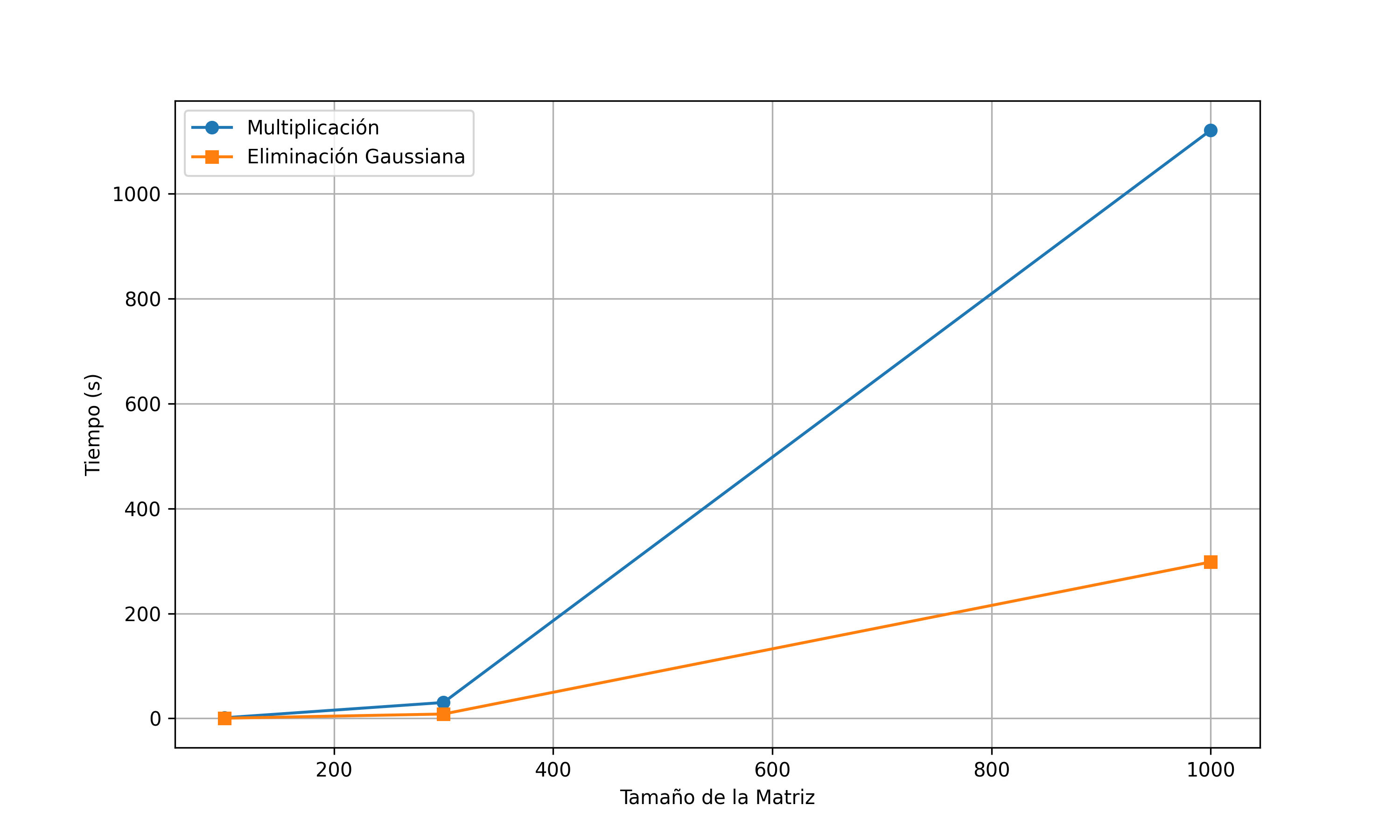{fig-align="center"}Entre los algoritmos restantes, **Quicksort** es el más rápido cuando P=512 ejecutandose en 0.013 segundos. Este resultado se debe a su eficiencia promedio de $O(n \log n)$ y al hecho de que en la mayoría de los casos selecciona pivotes efectivos para dividir los datos @loeser1974; @hoare1962. Sin embargo, en el peor caso, cuando los datos están desbalanceados, su complejidad puede degradarse a $O(n^2)$ \[@sedgewick2011\]. En las listas evaluadas cuando P=016 y P=032 su complejidad se lego a degradar llegando hasta un tiempo de ejecución de 0.21 segundos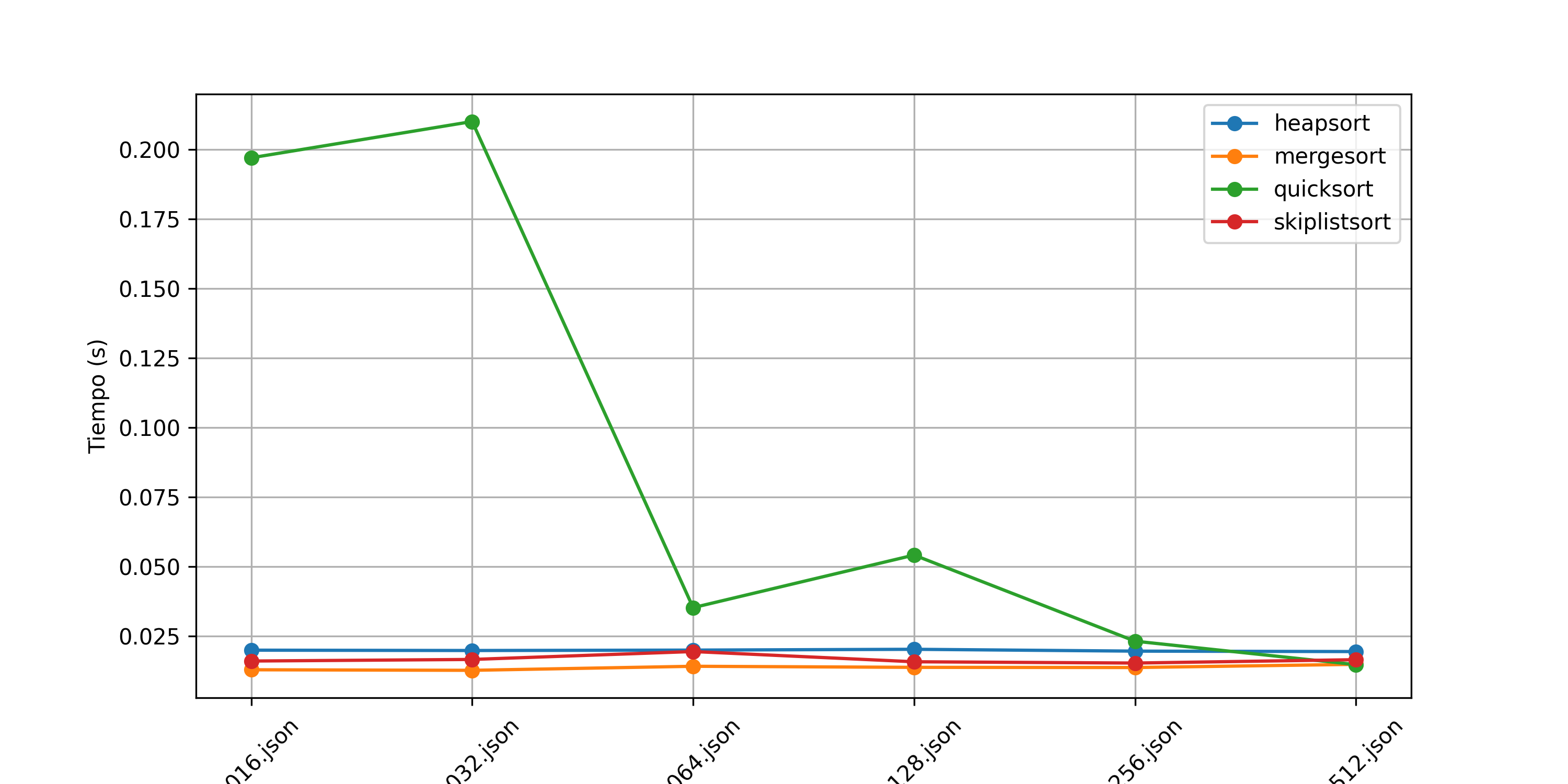{fig-align="center"}**Mergesort** presenta tiempos de ejecución ligeramente superiores a los de Quicksort, pero se mantiene en el mismo orden de magnitud. Su ventaja principal radica en su estabilidad y en su rendimiento predecible de $O(n \log n)$ en todos los casos, lo que lo hace ideal para aplicaciones donde la estabilidad es crítica, como la ordenación de registros de bases de datos [@knuth1998]. Se nota una tendencia a incrementar el tiempo de ejecución conforme va aumentando el nivel de desorden de los datos.**Heapsort** muestra tiempos de ejecución consistentes, pero es ligeramente más lento que Quicksort y Mergesort. Esto se debe a las operaciones de heapify, que introducen una mayor cantidad de operaciones en la manipulación de los datos, y tambien se nota un poco de mayor de tiempo en niveles de desorden bajos. Aunque su peor caso sigue siendo $O(n \log n)$, su overhead adicional lo hace menos competitivo en comparación con los otros métodos [@cormen2009].Finalmente, el algoritmo basado en **SkipList** tiene tiempos de ejecución intermedios, siendo más lento que Quicksort y Mergesort, pero similar a Heapsort, y se nota una tendencia estable en el tiempo de ejecución conforme va a aumentando el nivel de desorden de las listas. Esto se debe a la naturaleza probabilística de las listas enlazadas con múltiples niveles, las cuales requieren más operaciones para ordenar los datos [@pugh1990]. A pesar de ello, su rendimiento sigue siendo eficiente para estructuras dinámicas donde la inserción y búsqueda rápida son cruciales.## Número de ComparacionesEl número de comparaciones es una métrica crucial para evaluar la eficiencia de los algoritmos de ordenamiento, ya que está directamente relacionado con la complejidad computacional de cada método. En la **Tabla** \ref{tab:results1} se presentan los valores obtenidos para cada algoritmo en distintos tamaños de archivos, mientras que las **Figuras 3 y 4** muestran la comparación gráfica de estas operaciones.\input{resultados_comp.tex}Como se observa en la **Figura 3**, el algoritmo **Bubblesort** realiza un número extremadamente alto de comparaciones en comparación con los otros métodos. Su crecimiento cuadrático, con una complejidad de $O(n^2)$, provoca que el número de comparaciones aumente exponencialmente a medida que el tamaño del conjunto de datos se incrementa [@cormen2009], pero en este caso se llega a estabilizar en alrededor de 470000 sin importar el nivel de desorden de los datos. Debido a esta magnitud del Número de comparaciones, la **Figura 4** excluye Bubblesort para resaltar mejor el comportamiento de los otros algoritmos.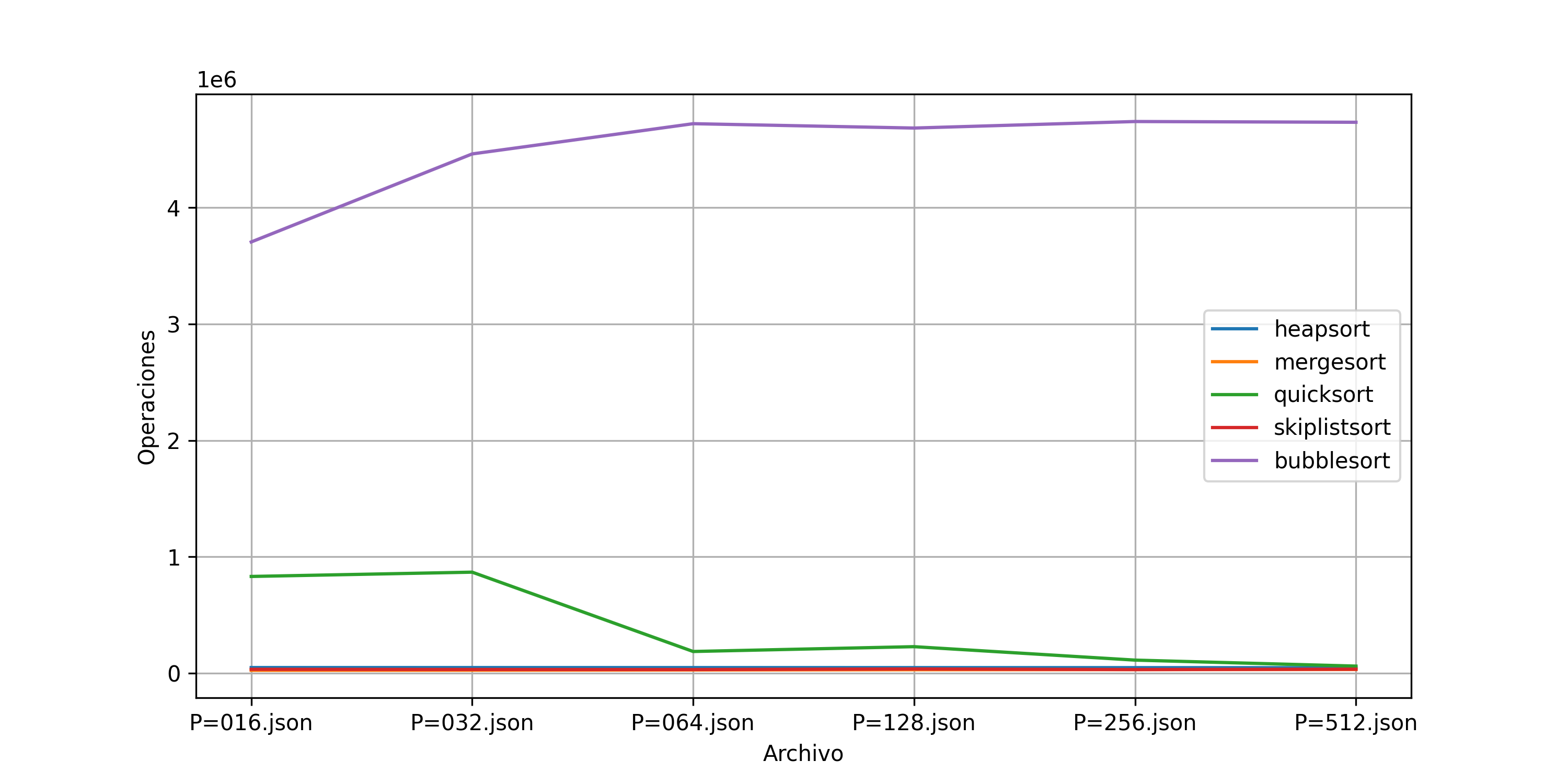{fig-align="center"}Entre los algoritmos restantes, **Mergesort** es el que realiza el menor número de comparaciones en todos los casos, lo que se debe a su estrategia de dividir y conquistar, logrando un rendimiento estable de $O(n \log n)$ en todos los escenarios [@knuth1998]. Esto confirma su idoneidad para situaciones donde el número de comparaciones es un factor limitante, como en el procesamiento de grandes volúmenes de datos en bases de datos y sistemas de archivos [@sedgewick2011]. De igual manera que con el tiempo de ejecución se observa un número de operaciones con tendencia a la alza conforme el nivel de desorden de los datos va aumentando.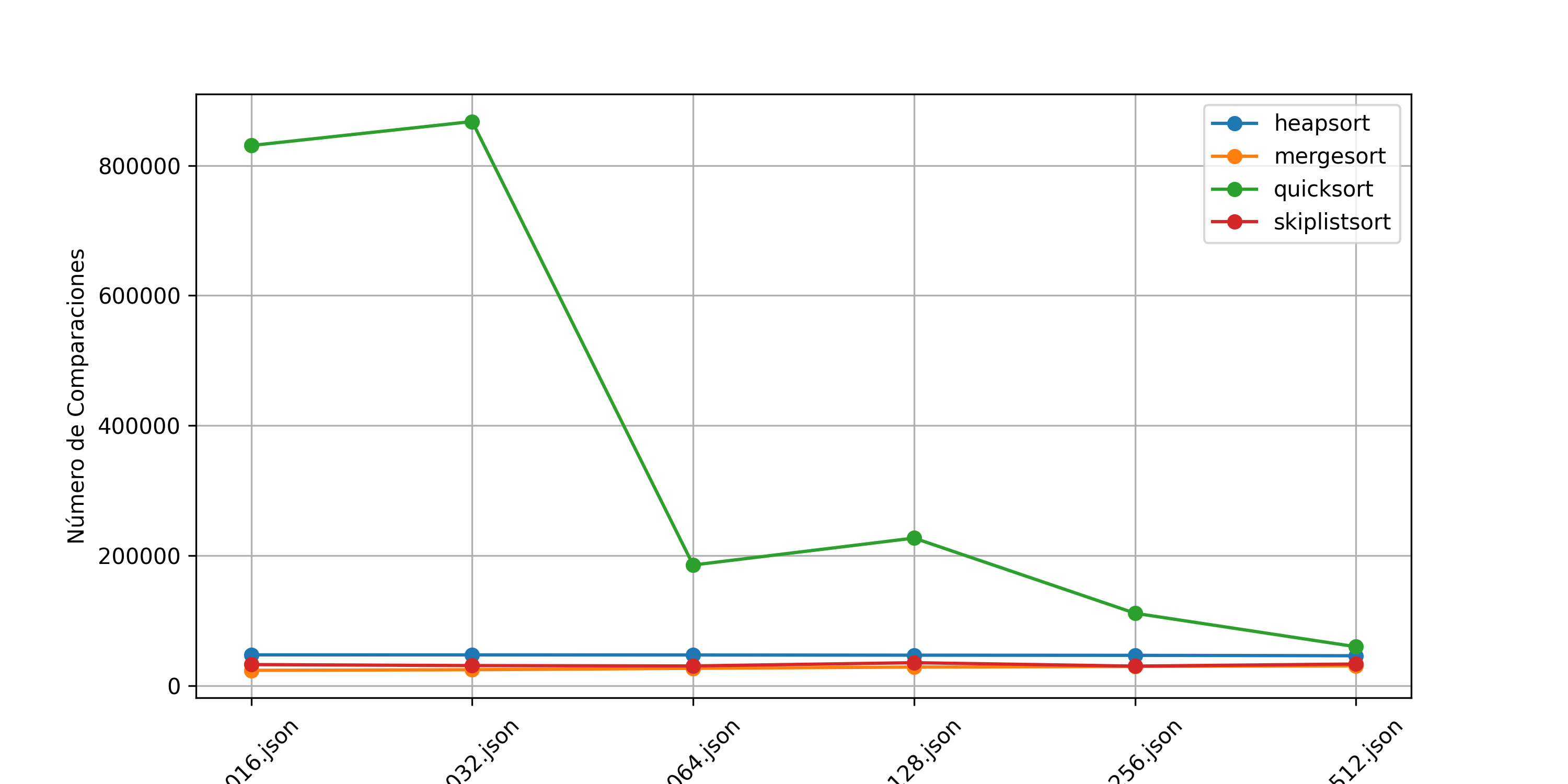{fig-align="center"}Por otro lado, **Quicksort** presenta un número de comparaciones en comparación con los demás algoritmos (excluyendo a Bubble Sort), pero sigue siendo bastante eficiente cuando las listas se van aumentando su nivel de desorden. Su complejidad promedio de $O(n \log n)$ lo hace competitivo, aunque en su peor caso puede alcanzar $O(n^2)$ si los pivotes seleccionados no dividen bien los datos [@hoare1962], este caso se presenta niveles bajos de desorden de las listas. En este caso el número de comparaciones va disminuyendo conforme P va aumentando en las listas.**Heapsort** realiza un número de comparaciones mayor que Quicksort y Mergesort, lo que se debe a la naturaleza de la estructura de montículo utilizada para mantener el orden de los elementos. Su comportamiento es consistente y su peor caso sigue siendo $O(n \log n)$, pero su mayor número de comparaciones lo hace menos competitivo en comparación con los otros métodos [@cormen2009]. Se nota una tendencia estable conforme va aumentando el nivel de desorden de las listas.El algoritmo **SkipListSort** muestra un comportamiento más variable en términos de comparaciones, con fluctuaciones en distintos tamaños de datos y niveles de desorden. Esto se debe a la naturaleza probabilística de las listas enlazadas en múltiples niveles, que introducen cierta incertidumbre en el número de operaciones requeridas para ordenar los elementos [@pugh1990]. A pesar de estas variaciones, su número de comparaciones sigue siendo relativamente cercano a los otros algoritmos eficientes y es significativamente menor que el de Bubblesort.# ConclusiónEn conclusión, Quicksort es el algoritmo más eficiente en términos de tiempo de ejecución cuando las listas presentan alto nivel de desorden. Para el caso de Mergesort y Heapsort son medianamente eficientes y el nivel de desorden no afecta degrada su complejidad. SkipListSort se comporta de manera aceptable, pero no es tan eficiente como los métodos clásicos de comparación. Bubblesort, en contraste, es altamente ineficiente y se vuelve impráctico para grandes volúmenes de datos. Estos resultados coinciden con estudios previos sobre la eficiencia de los algoritmos de ordenamiento y confirman la superioridad de los métodos basados en división y conquista para el procesamiento eficiente de datos [@sedgewick2011].El análisis de comparaciones confirma que **Bubblesort es altamente ineficiente**, mientras que **Mergesort y Quicksort son los métodos más efectivos** en términos de reducir el número de operaciones. **Heapsort** tiene un desempeño estable pero menos competitivo, y **SkipListSort muestra variabilidad en su número de comparaciones** debido a su estructura de datos probabilística. Estos resultados refuerzan los estudios previos sobre la eficiencia de los algoritmos de ordenamiento y su aplicabilidad en distintos escenarios computacionales [@sedgewick2011].##Lista de Cambios- Se implementó quicksort in-place usando el esquema de partición de Lomuto, con el último elemento como pivote.- Se implementó mergesort in-place usando índices, evitando la creación de nuevas listas en cada llamada recursiva.- Cambios en Analisis de Resultados asi como conclusiones con nuevos resultados de Quicksort y Merge Sort# Bibliografía